
Pyramid logo
introductory fermentation bag
what materials are needed
Required:
- Dry active yeast (one 4 oz. jar contains approximately 36 teaspoons of yeast, which will make 36 bags)
- Warm water source
- Small graduated cylinders (100mL)
- Measuring spoons (one teaspoon for each feedstock source and the yeast to avoid cross-contamination)
- Feedstock(s): sugar, cornmeal, corn stover, sawdust, etc.
- Resealable zipper bags (“snack" size) with fill-in labels (see Supplementary Materials for label template).
Recommended:
- Rulers to measure bag inflation. See Supplementary Materials for instructions.
- Classroom-grade ethanol probe (Vernier or PASCO) or breathalyzer for detecting ethanol levels. See Supplementary Materials for instructions.
- 2-4 liter thermos (with spout) for dispensing warm tap water
- Paper towels
- print this data collection sheet
Pre-experiment questions
- What food source will you give to your yeast?
- What changes, if any, do you expect to observe with your bag over time?Explain.
- Do you expect to see any differences in observations between food sources that your class is comparing? Explain.
During experiment questions
During the experiment: Record your observations and measurements.
Yeast food source: _______________________
Start time:__________ End time:__________ Total time (min):___________
| Observations & Measurements: | Before | After |
|---|---|---|
| Record scientific observations & measurements (changes in appearance, smell, etc) |
what are the steps
1. In a snack-size resealable zipper bag, combine 1 teaspoon of sugar (or another feedstock) and 1 teaspoon of yeast.
2. Add 50 mL (1/4 cup) of warm tap water (approx 40° C) and seal bag closed, removing as much air as possible.
3. Mix gently. Lay bag on a flat surface and watch for results – fastest results should be achieved in 15 minutes.**
4. Optional: Measure and compare ethanol and/or CO2 production using ethanol probes, breathalyzers, rulers, etc. Discuss and interpret results.
break point: 45 minute lesson plan
After experiment questions
After the experiment: Analyze and interpret your results.
Summarize what you know about substances in the bag before and after the experiment using this table:
| Questions | Start of experiment | After experiment |
|---|---|---|
| What's in the bag? | ||
| What evidence do you have? |
Propose an explanation for the changes you observed.
Compare your results with the class. What differences did you observe between food sources made of sugar, starch or cellulose?
Propose an explanation for those differences.
break point: 45 minute lesson plan
Class room variations: Guided inquiry
Reference: classroom variations
Overview: Fermentation with a Bag, Bottle and Balloon
Students work in small groups (“research teams") to investigate two guiding questions:
1.) “Which feedstock will produce the largest volume of CO2 gas?"
2.) “What methods could be used to collect data to measure volume of CO2 produced?"
Student teams are given flexibility to choose research questions, feedstock options and data collection methods. Example feedstocks could include, ripe versus unripe bananas, breakfast cereals, sugar, corn starch, sawdust, etc.
Example data collection could include measuring bag volume, time to bag inflation, balloon ininflation circumference, or Vernier CO2 gas pressure sensors.
Suggested materials
Suggested Materials and Supplies:
The suggested materials and supplies listed are necessary to provide flexibility in the inquiry lab.
Teachers may choose to limit the supplies due to time and developmental needs of students. The basic supply list includes the feedstock, containers and simple means to measure the volume/production of CO2 gas.
Classrooms with ethanol, CO2 or pressure probes may choose to use them to provide a more exact data measurement. Various solutions and the use of fruit for a feedstock are options for an extension to the lab presented here.
Instructors and students are encouraged to be creative with investigating different feedstock options, measurement techniques and the effects of different treatments.
Materials:
- Feedstock options: Corn starch, sugar, saw dust, snack bag sample of dierent cereals (with nutrition label), (optional): ripe & unripe banana
- Solution: Water, salt (optional), corn syrup (optional)
- Microbes: Yeast
- Glassware: 250ml Erlenmeyer Flasks or at bottom test tubes/round test tube, test tube holders
- Other: Snack size and Quart size Ziploc bags, balloons , graduated cylinders, measuring spoons,
- thermometers, Optional:s, rubber tubing, tape measure, gram scale.
- Safety: Goggles required
Procedure
The following procedure for guiding students through this investigation is presented based on the “5E Instructional Model," this procedure can easily be adapted to different instructional approaches. Learn more about this instructional model here: http://www.bscs.org/bscs-5e-instructional-model.
ENGAGE:
- Prior to the introduction of this lab, students are asked to bring in one small snack size baggie with a favorite cereal and a copy or cutout of the nutrition label.
- Upon entering the classroom, students participate in a shortened version of the traditional GLBRC lab, “Fermentation in a Bag." This was used as a “Science Starter" or warm-up activity.
- An overview of the unit is provided after discussing the initial Fermentation in a Bag activity.
- Two essential questions are asked:
- “Which feedstock/cereal will produce the largest volume of CO2gas?" and,
- “How can data/evidence be collected to measure CO2 gas?"
- Prior to division into “research teams" a review of materials/supplies, procedures and safety procedures is provided.
- In small groups, students are asked to brainstorm their own questions which could lead to an investigation. (Optional: Distribute a “ClaimsEvidence-Reasoning" sheet to structure student investigation).
EXPLORE:
- Divided into research teams, students complete the following steps as they plan and carryout their investigation:
- BRAINSTORM AT LEAST TEN RESEARCH QUESTIONS. SELECT ONE QUESTION TO INVESTIGATE. (Example: How does temperature affect CO2 gas production).
- MAKE A CLAIM.
- IDENTIFY DEPENDENT & INDEPENDENT VARIABLES.
- DECIDE HOW TO MEASURE YOUR DEPENDENT VARIABLE.
- DESIGN AN INVESTIGATION THAT WILL PROVIDE RICH DATA (EVIDENCE) IN A CONTROLLED EXPERIMENT.
- CHECK WITH THE INSTRUCTOR BEFORE BEGINNING YOUR INVESTIGATION.
- CONDUCT AN INVESTIGATION WITH A CONTROL
- COLLECT DATA
- DISPLAY DATA
- PRESENT: USE DATA TO SUPPORT OR REFUTE YOUR CLAIM.
EXPLAIN:
Research teams present preliminary findings during an informal data presentation session.
Teams are asked to restate their “claim" or hypothesis, describe or prepare a data table or graph with their data and provide their reasoning for their results using the data they collected.
EXTEND:
(Optional-time permitting) Students may refine or extend their investigations
to explore new questions or collect new data with revised procedures based on what
they learned in their first investigation.
EVALUATE:
Students summarize findings across all research investigations. Teachers
may provide an exit slip or ask students to provide a brief response to questions from
the investigation.
Engineering estimation
Designing experiments and recording observed measurements requires creative scientific skills. Using experimental data to make estimation and predictions is equally creative for combining science, engineering, math and statistics.
Watch this video of a person estimating the number of grains of sand in the Sahara desert.
If you found this video clever and want to learn how to think like this, try this problem below. You should also let your teacher know you like this or send us a message here to chat more about professions that seek people with this curiosity for scientific estimation.
Thinking creatively like this by combining biology with math, chemistry and physics are skills anybody can learn.
And there are professions that seek people who can creatively combine these skills to solve societal challenges facing people, animals, habitats.
If you like these types of challenges but think you're not good in math, chemistry and physics to be any good, give yourself the chance to apply these skills in real world problems. You might find with after a few years of practice, you'll be doing these things in your head.
The story and challenge...
You know that ethanol is a type of alcohol can kill the coronavirus.
And you now know that yeast can metabolize sugar to create ethanol.
So what if in a future coronavirus pandemic, there was a shortage shortage of ethanol, what would you do?
But before you started telling people you could help, you wanted to not overpromise how much you could help. So you decide to estimate how much ethanol you could produce in ziplock bags
How would you estimate this?
In this experiment you found in 30 minutes that ______________ grams of yeast + _____________ grams of sugar made a ziplock bag fill with carbon dioxide.
But how do you figure out how much ethanol is in the bag?
Well, what would you do if you had this stoichiometric equation?
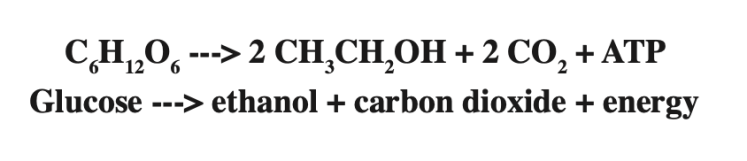
What if we were to say that all of the grams of glucose were converted to ethanol? How many grams of ethanol would you estimate are in your bag?
How many glucose molecules are in a gram of glucose?
| Glucose | C6H12O6 | ||
| Element | Number of atoms |
Molar mass [grams/mol] |
Molar mass subtotal [grams/mol] |
| Carbon | 6 | 12 | 72 |
| Hydrogen | 12 | 1 | 12 |
| Oxygen | 6 | 16 | 96 |
| Total mass | 180 |
So if 1 mole of glucose has a molar mass of 180 grams/mol, then how many glucose molecules are in 1 gram?
(1 grams glucose)/(180 grams glucose/mol) = 0.0055 moles
How many glucose molecules are in 0.0055 moles?
- 3.34 x 1021 molecules of glucose
If yeast converts 1 molecule of glucose into 2 molecules of ethanol, how many ethanol molecules are in the bag containing 1 gram of glucose? 6.68 x 1021 molecules of ethanol
If you have a different mass of glucose in your bag, how many grams of ethanol are in your bag?
| Ethanol | CH3CH2OH | ||
| Element | Number of atoms |
Molar mass [grams/mol] |
Molar mass subtotal [grams/mol] |
| Carbon | 2 | 12 | 24 |
| Hydrogen | 6 | 1 | 6 |
| Oxygen | 1 | 16 | 16 |
| Total mass | 46 |
(0.0055 mol of glucose) x (2 mol of ethanol/1 mol of glucose) = 0.011 mol of ethanol
(0.011 mol of ethanol) x (46 grams of ethanol/mol of ethanol) = 0.506 grams of ethanol
How many liters of ethanol is in your bag?
What physical property has an equation that relates mass to liters?
(0.506 grams of ethanol)x(789.3 grams of ethanol/liter of ethanol) = 0.000641 liters of ethanol = 0.641 mL
We're estimating. So how many significant digits should you report? 0.641 mL, 0.64 mL, 0.6 mL?
So if a nurse in a hospital needs to wash their hands with 100 mL of alcohol before touching a patient and one nurse typically attends to 100 patients per day, how much ethanol does one nurse need per day?
How many bags of yeast+glucose do you need to need to produce enough ethanol for one nurse?
If there are 100 nurses in the hospital, how many bags of yeast+glucose do you need to make per day to provide for all the nurses?
If ethanol occupies 0.641 mL in the bag, how would you calculate how many liters of carbon dioxide is in the bag?
If you had a bucket and water, how might you experimentally calculate how much carbon dioxide is in the bag?
First measure the mass of the bucket on a scale.
Next fill the bucket to the rim with water measure the mass again.
Subtract the difference. This is equal to the mass of water.
From the density equation, you can calculate the volume of water in a bucket even if it has tapered or irregular shape.
Without spilling any water, remove the bucket from the scale and place it in a location where it's okay for things to get wet.
Now ensure your ziplock bag is sealed tight. Slowly submerge it into the bucket of water. The displaced water will spill onto the floor.
Remove the bag from and gently place the bucket with remaining water back onto the scale.
Subtract this mass measurement from the original mass of the empty bucket.
Subtracting the mass of the full bucket of water from the mass of the bucket after water was displaced by the bag gives you the mass of water that would have occupied the volume of the ziplock bag.
Using the density of water equation, you can now solve for volume of the ziplock bag containing CO2.
Subtract the volume of ethanol you calculated above from this experimental volume measurement of the bag. This gives you approximately the volume of CO2. (A small difference will be due to the volume in the bag occupied by the yeast and water)
Now rearrange the ideal gas law to find the number of moles of carbon dioxide: PV = nRT
You can make some measurements about the temperature and atmospheric pressure in the room.
Compare the number of moles and mass of CO2 calculated experimentally to the number of moles and mass of CO2 you calculated using the stoichiometry equation method.
Why might it not be safe to use alcohol produced by yeast without purification?
If it takes 30 minutes for yeast to reproduce and we stop the experiment at 29.999 minutes, then is the final number of yeast cells greater, equal to, or less than the initial number of yeast cells?
If we approximate a yeast cell as having a mass of 60 picograms (pg) 60x10-12 and we placed 1 gram of yeast into the bag, then approximately how many yeast cells are in the bag at time = 29.999 minutes?
(1 gram yeast)/(6.0x10-11 grams per yeast cell) = 1.67 x 1022 yeast cells
If after 29 minutes there is 6.68 x 1021 molecules of ethanol then on average how many molecules of ethanol did each yeast cell produce in the 29.999 minute time period?
(6.68 x 1021 molecules of ethanol)/(1.67 x 1022 yeast cells) ~ 4 x 10-1 ethanol molecules per yeast cell per ~30 minute time period. Let's allow ourselves to round this to 5 x 10-1 ethanol molecules per yeast cell per ~30 minute time period. Or 0.5 ethanol molecules per yeast cell per ~30 minutes. 0.5 or 1/2 is an easier number to keep in our memory.
It is still odd to think about 0.5 molecules being produced per yeast cell in 30 minutes. A more intuitive way to express this is to say in a 30 minute time period only half of the yeast cells produce an ethanol molecule.
An analogy is to think about baking cakes. Imagine a 24 hour bake-a-thon consistin of 10 bakers. You stop in to the competition for 30 minutes and count how many cakes are completed in the 30 minutes you are present. If 10 bakers completed 5 cakes in 30 minutes, we could say that each baker baked 0.5 cakes in 30 minutes. That's an odd way to think about making cakes. Just like it's odd to think about 1/2 of a molecule of ethanol being produced in 30 minutes. Another more intuitive way to express this is to say that if in a randomly selected 30 minuted time period you only saw 5 cakes being made by 10 bakers, we could estimate that it takes each baker 60 minutes to make a cake.
So if we've rounded to 0.5 molecules of ethanol produced by 1.67 x 1022 yeast cells in a 30 minute time window, then we can say that it takes 60 minutes for each yeast cell to produce one molecule of ethanol.
You can develop a deeper appreciation for individual cells by using basic math, physics, chemistry and biology principles to each cell's capability.
Step back for a moment and ask yourself these questions:
- Did you find it interesting to measure the height of the bag when using different feedstocks?
- How did estimating the amount of ethanol molecules help you apply your experimental observations to an societal challenge such as coronavirus hospital hygiene?
- If you someone were to say to you that a kilogram of yeast could provide enough ethanol to fill a 10 liter fuel tank in 5 hours, would you be able to estimate whether their statement is plausible?
- Without experimental data to provide evidence, can you think of another way to make estimates to check the plausibility of claims such as ethanol for biofuels and hospital hygiene?
Commentary and modifications
With the constrains of a typic science classroom, there is rarely enough time, money for supplies or capability for students to do more than surface-level investigations. In this lab, teachers may allow students to design most phases of a true investigation including how to collect data, design and standardize procedures and ask questions that lead to investigations.
Adding cereal as a feedstock to this lab added high interest for students and
provided a surprising nding. In their lab, students found that Cheerios produced more CO2 than Corn Pops. This led to a better comparison of the sugar content by weight andvolume on the cereal labels.
When time is limited, teachers may select the data collection method of choice using 9" balloons (check for latex allergies) or probes (CO2/pressure) from the lab.
To further limit time, teachers may choose to allow a group brainstorm of research questions and then select one or two from the list that all groups will investigate.

